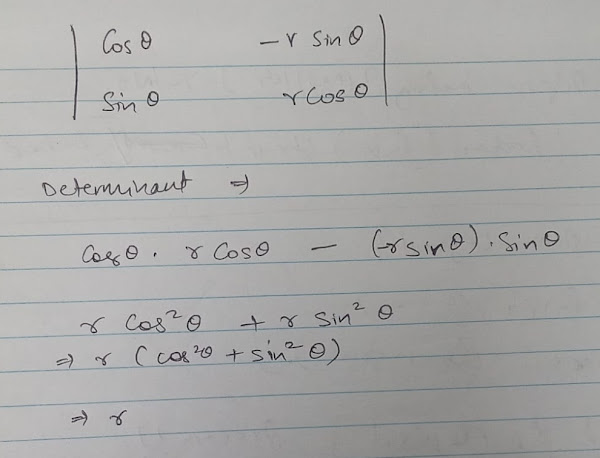Sunday, January 7, 2024

Exercise 1.4 On Probability Densities - Pattern Recognition and ML - By Christopher Bishop

Pre-read
Fig:1


Fig:2


Fig:3


If we have several continuous variables x1,...,xD, denoted collectively by the vector x, then we can deﬁne a joint probability density p(x) = p(x1,...,xD) such

Fig:4


Question

Fig:5


Solution

Exercise 1.5 On Concept of Variance From Statistics - Pattern Recognition and ML - By Christopher Bishop

Pre-read




1.5: Using the deﬁnition (1.38) show that var[f(x)] satisﬁes (1.39).

Solution

Exercise 1.6 On Covariance - Pattern Recognition and ML - By Christopher Bishop

Pre-read
Fig 1



Fig 2



1.6: Show that if two variables x and y are independent, then their covariance is zero.

Solution

Fig 3



Fig 4

Exercise 1.7 - Identifying normalization constant for Gaussian Distribution and Proving that it's integral equals 1 - From Pattern Recognition and ML - By Christopher Bishop

Pre-read

Fig 1:

Fig 2:

Question

Fig 3:

Solution

Fig 4:

Fig 5:

Fig 6:

Fig 7:

Fig 8:

Fig 9:

Fig 10:

Fig 11:

Index of Machine Learning

Toggle All Sections

THEORY

What is Machine Learning?

What is Machine Learning (With Video and Interview Questions)

Logistic Regression

Decision Tree

Decision Tree (Using Gini Impurity) - With Video and Interview Questions

Deep Learning

But what is a neural network? | Chapter 1, Deep learning

Integration

Vector Calculus

Exercises from the book "Pattern Recognition and Machine Learning" by Christopher Bishop

Statistics

PRACTICALS

ML1: Category Encoding

ML2: Data Preprocessing

ML3: Data visualization

ML3.1: Misc

ML3.2: Using PowerBI

ML3.3: Line Chart

ML3.4: Pie Plot

ML3.5: Choropleth and Cartography

Choropleth: A choropleth map is a type of statistical thematic map that uses pseudocolor, i.e., color corresponding with an aggregate summary of a geographic characteristic within spatial enumeration units, such as population density or per-capita income. 
Cartography: the science or practice of drawing maps.

ML3.6: Histogram

ML4: Outlier Detection / Anomaly Detection

ML5: Classification

ML5.1: Decision Tree

ML5.2: Miscellaneous of Classification

ML6: Clustering

ML7: Regression

ML8: Association Mining Between Attributes

ML9: Weka Tool

ML10: Traffic Prediction on my Blog

ML11: Questions and Answers

ML12: Miscellaneous

ML13: Articles

ML14: Our 'Machine Learning' Videos on YouTube

Thursday, December 28, 2023

Mushroom Picker (A problem on Prefix Sums)

Problem

You are given a non-empty, zero-indexed array A of n (1 <= n <= 100000) integers a0, a1,..., an−1 (0 <= ai <= 1000). This array represents number of mushrooms growing on the consecutive spots along a road. You are also given integers k and m (0 <= k, m < n).

A mushroom picker is at spot number k on the road and should perform m moves. In one move she moves to an adjacent spot. She collects all the mushrooms growing on spots

she visits. The goal is to calculate the maximum number of mushrooms that the mushroom

picker can collect in m moves.

For example, consider array A such that:

A[0]=2, A[1]=3, A[2]=7, A[3]=5, A[4]=1, A[5]=3, A[6]=9

The mushroom picker starts at spot k = 4 and should perform m = 6 moves. She might

move to spots 3, 2, 3, 4, 5, 6 and thereby collect 1 + 5 + 7 + 3 + 9 = 25 mushrooms. This is the

maximal number of mushrooms she can collect.

Code

# Counting preﬁx sums
  def prefix_sums(A):
      n = len(A)
      P = [0] * (n + 1)
      for k in xrange(1, n + 1):
          P[k] = P[k - 1] + A[k - 1]
      return P
  
  # Total of one slice
  def count_total(P, x, y):
      return P[y + 1] - P[x]
  # Mushroom picker — O(n + m)
  def mushrooms(A, k, m):
      n = len(A)
      result = 0
      pref = prefix_sums(A)
  
  # When we first take p steps on the left and return from their back in right direction.
      for p in xrange(min(m, k) + 1):
          left_pos = k - p
          right_pos = min(n - 1, max(k, k + m - 2*p))
          result = max(result, count_total(pref, left_pos, right_pos)) 
  
  # When we first take p steps on the right and return from their back in left direction.
      for p in xrange(min(m + 1, n - k)):
          right_pos = k + p
          left_pos = max(0, min(k, k - (m - 2*p)))
          result=max(result, count_total(pref, left_pos, right_pos)) 
      return result

Explanation (Part 1)

# When we first take p steps on the left and return from their back in right direction.
    for p in xrange(min(m, k) + 1):
        left_pos = k - p
        right_pos = min(n - 1, max(k, k + m - 2*p))
        result = max(result, count_total(pref, left_pos, right_pos))

Expression “for p in xrange(min(m, k) + 1)” has min(m, k) because we can only go m steps to the left or k steps to the left whichever number is minimum.

After going k steps, we cannot go past 0th position.

Or after taking m steps, we cannot take another step.

Expression “right_pos = min(n - 1, max(k, k + m – 2*p))” has ‘k+m-2*p’ because after taking p steps to the left, we are returning p steps back to position k, hence 2p.

And then number of steps left is: m – 2p

Then right position is identified by: m-2p steps after k ie, k+m-2p

Expression “right_pos = min(n - 1, max(k, k + m – 2*p))” has max(k, k + m – 2*p) because what if we take all the m steps to left and value of p becomes m.

Then there are no steps left to take to the right and right position is simply identified by k.

Similarly, for any value of p > m/2 (as in 0.6m or 0.75m), we would get same right position as k.

Explanation (Part 2)

# When we first take p steps on the right and return from their back in left direction.
    for p in xrange(min(m + 1, n - k)):
        right_pos = k + p
        left_pos = max(0, min(k, k - (m - 2*p)))
        result = max(result, count_total(pref, left_pos, right_pos))

Here in the expression “for p in xrange(min(m + 1, n – k))”, we have m+1 and not just m because xrange goes till m when passed the argument m+1. Similarly, we have n-k and not (n-1)-k because xrange goes till (n-1)-k when passed the argument n-k.

And we take minimum of m or (n-1)-k because that’s is the possible number of steps we can take on the right.

Here in the expression “left_pos = max(0, min(k, k - (m – 2*p)))”, we have k-(m-2p) because we take p steps on the right, then take those p steps back to k (on the left now).

Number of steps yet to take: m-2p

Left position would be identified by: k-(m-2p)

If p takes value m, which means we have taken m steps on the right, then we have no steps remaining to take to the left and left position is identified by k itself. (This logic is valid for any value of p > m/2)

Side Note

The way we calculating prefix sums and sums of subsections is without using the Python built-ins. But if we were to use Python built-ins, the code would look somewhat like this:

def get_mushrooms_sum(A, start, end):
  return sum(A[start : end + 1])

Coding Round in Interview for Data Scientist Role at a Bank (17 Nov 2023)

Task 1

Write a function:

    def solution(A)

that, given an array A of N integers, returns the smallest positive integer (greater than 0) that does not occur in A.

For example, given A = [1, 3, 6, 4, 1, 2], the function should return 5.

Given A = [1, 2, 3], the function should return 4.

Given A = [−1, −3], the function should return 1.

Write an efficient algorithm for the following assumptions:

        N is an integer within the range [1..100,000];
        each element of array A is an integer within the range [−1,000,000..1,000,000].

A brute-force solution to this problem that will fail the performance tests will look like this:


def solution(A):
    # a_sort = sorted(A)
    rtn = -1
    for i in range(1, 100001):
        if i in A: # This is the most time consuming instruction of this code that runs repeatedly for all of i(s)
            continue
        else:
            rtn = i
            break
    return rtn 


Task 2




Task 3

Fig 3.1



Fig 3.2



Fig 3.3

Monday, December 25, 2023

Building a Tree from a BODMAS Expression (An exercise in Recursion)

There is an expression with N variables as in A, B, C, X, Y, Z. Note that variables do not repeat. And N-1 variables which can be +,-,*, and /

For example:

Ex 1: X + Y * Z
Ex 2: X - Y * Z + A
Ex 3: X * Y - Z / A
Ex 4: X / Y / Z
Ex 5: X * Y / Z
Ex 6: Z - Y + X

Now, can you give me a recursion based JavaScript code to create a tree with operators on non-leaf nodes and leaf nodes contains the variables based on the BODMAS evaluation of the expression.

Code Pre-read

Certainly! To represent an expression as a tree structure in JavaScript, you can use a recursive data structure. Here's a simple example of how you can create a tree with operators on non-leaf nodes and variables on leaf nodes based on BODMAS evaluation:

…

Code in on next slide

This code defines a TreeNode class to represent nodes in the expression tree. The buildExpressionTree function takes an expression as input and returns the root of the expression tree. The tree is built recursively based on the BODMAS rules, with operators on non-leaf nodes and variables on leaf nodes.

Note: This code assumes that the input expression is properly formatted and follows BODMAS rules.

Code to Build a Tree Node

class TreeNode {
    constructor(value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

Code

function buildExpressionTree(expression) {
  // Tokenize Expression
  const tokens = expression.split(/\s/).filter(token => token.trim() !== ''); 

    
    // Helper function to build the expression tree recursively
    function buildTree(start, end) {
        if (start === end) {
            // Base case: single variable
            return new TreeNode(tokens[start]);
        }

        // Find the operator with the lowest precedence
        let minPrecedence = Infinity;
        let minIndex = -1;
        
        for (let i = start; i < end; i++) {
            if (tokens[i] === '+' || tokens[i] === '-') {
                const precedence = 1;
                if (precedence <= minPrecedence) {
                    minPrecedence = precedence;
                    minIndex = i;
                }
            } else if (tokens[i] === '*' || tokens[i] === '/') {
                const precedence = 2;
                if (precedence <= minPrecedence) {
                    minPrecedence = precedence;
                    minIndex = i;
                }
            }
        }
// Create the current node with the operator
        const currentNode = new TreeNode(tokens[minIndex]);

        // Recursively build left and right subtrees
        currentNode.left = buildTree(start, minIndex - 1);
        currentNode.right = buildTree(minIndex + 1, end);

        return currentNode;
    }

    // Build the tree starting from the root
    return buildTree(0, tokens.length - 1);
}

// Example usage:
const expression = "X + Y * Z";
const expressionTree = buildExpressionTree(expression);
console.log(expressionTree);

Explanation of the code

Certainly! Let's go through the code line by line:

TreeNode Class

class TreeNode {
    constructor(value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

This part defines a TreeNode class, which will be used to represent nodes in the expression tree. Each node has a value (either an operator or a variable), a left child, and a right child.

function buildExpressionTree(expression) {
    const tokens = expression.split(/\s/).filter(token => token.trim() !== ''); // Tokenize expression

    The buildExpressionTree function takes an input expression and splits it into tokens using a regular expression. The regular expression \b matches word boundaries, and filter is used to remove any empty or whitespace-only tokens.


    // Helper function to build the expression tree recursively
    function buildTree(start, end) {
        if (start === end) {
            // Base case: single variable
            return new TreeNode(tokens[start]);
        }

    The buildTree function is a helper function for building the expression tree recursively. The base case checks if start and end are the same, which means we have reached a leaf node containing a single variable. In this case, a new TreeNode is created with the variable as its value.

Operator Precedence
Next, we are going to look at operator precedence.
Viz:
In the order DM > AS 
And if it’s DD or MM or DM, then left to right.
        // Find the operator with the lowest precedence
        let minPrecedence = Infinity;
        let minIndex = -1;
        
        for (let i = start; i < end; i++) {
            if (tokens[i] === '+' || tokens[i] === '-') {
                const precedence = 1;
                if (precedence <= minPrecedence) {
                    minPrecedence = precedence;
                    minIndex = i;
                }
            } else if (tokens[i] === '*' || tokens[i] === '/') {
                const precedence = 2;
                if (precedence <= minPrecedence) {
                    minPrecedence = precedence;
                    minIndex = i;
                }
            }
        }

    This part of the code searches for the operator with the lowest precedence in the given range (start to end). It iterates through the tokens, updating minPrecedence and minIndex whenever it finds an operator with lower precedence.



        // Create the current node with the operator
        const currentNode = new TreeNode(tokens[minIndex]);

        // Recursively build left and right subtrees
        currentNode.left = buildTree(start, minIndex - 1);
        currentNode.right = buildTree(minIndex + 1, end);

        return currentNode;
    }

    Once the operator with the lowest precedence is found, a new TreeNode is created with that operator as its value. The left and right children of this node are then recursively built using the buildTree function.
    // Build the tree starting from the root
    return buildTree(0, tokens.length - 1);
}

    Finally, the buildExpressionTree function initiates the construction of the expression tree by calling buildTree with the entire range of tokens. The function returns the root of the expression tree.



// Example usage:
const expression = "X + Y * Z";
const expressionTree = buildExpressionTree(expression);
console.log(expressionTree);

    This part demonstrates the usage of the code by creating an example expression ("X + Y * Z") and building an expression tree from it. The resulting tree is then printed to the console. The example expression can be replaced with other expressions as needed.

Overall, this code recursively builds an expression tree based on the BODMAS rules, where operators are placed on non-leaf nodes and variables on leaf nodes.

Prompts we tried on ChatGPT

There is an expression with N variables as in A, B, C, X, Y, Z. And N-1 variables which can be +,-,*, and /

For example:

Ex 1: X + Y * Z
Ex 2: X - Y * Z + A
Ex 3: X * Y - Z / A
Ex 4: X / Y / Z
Ex 5: X * Y / Z
Ex 6: Z - Y + X

A problem can have from 1 to 5 operators.

Now, can you give me a recursion based Python code to create a BODMAS based parenthesized expression for the given expression.

Bubble Sort (Using Recursion)

Can you give me python code for bubble sort?

Bubble sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. The pass through the list is repeated until the list is sorted.

Here's a simple Python implementation of the bubble sort algorithm:


def bubble_sort(arr):
    n = len(arr)

    # Traverse through all array elements
    for i in range(n):
        # Last i elements are already in place, so we don't need to check them
        for j in range(0, n-i-1):
            # Swap if the element found is greater than the next element
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

# Example usage:
my_list = [64, 25, 12, 22, 11]
bubble_sort(my_list)

print("Sorted array:", my_list)


This code defines a function bubble_sort that takes a list as input and sorts it in ascending order using the bubble sort algorithm. The example usage shows how to sort an example list, and the sorted array is then printed.

Using recursion?

Although bubble sort is not typically implemented using recursion due to its inefficiency compared to iterative methods, it can be done for educational purposes. Here's an example of a recursive implementation of bubble sort in Python:


def recursive_bubble_sort(arr, n=None):
    # Base case: If the array is empty or contains only one element, it is already sorted
    if n is None:
        n = len(arr)
    
    if n <= 1:
        return
    
    # One pass of bubble sort: Traverse the array and swap adjacent elements if they are in the wrong order
    for i in range(n - 1):
        if arr[i] > arr[i + 1]:
            arr[i], arr[i + 1] = arr[i + 1], arr[i]

    # Recursively call the function with a reduced size of the array
    recursive_bubble_sort(arr, n - 1)

# Example usage:
my_list = [64, 25, 12, 22, 11]
recursive_bubble_sort(my_list)

print("Sorted array:", my_list)

In this recursive implementation, the function recursive_bubble_sort takes an additional parameter n to represent the size of the array being considered in each recursive call. The base case checks if the array size is 1 or less, in which case the array is considered sorted. Otherwise, one pass of the bubble sort is performed, and the function is called recursively with a reduced size of the array.

What is the time complexity of the recursion based code?

The time complexity of the recursive version of bubble sort remains O(n^2) in the worst and average cases, just like the iterative version. This is because, even though recursion is used, the number of comparisons and swaps required to sort the array is still proportional to the square of the number of elements in the array.

Each recursive call performs one pass through the array, and there are a total of n recursive calls (each reducing the size of the array by 1). In each pass, the algorithm compares and potentially swaps adjacent elements, and this process is repeated for each pass until the array is sorted.

Therefore, the overall time complexity is still O(n^2), which makes bubble sort, whether implemented iteratively or recursively, inefficient for large datasets compared to more advanced sorting algorithms like quicksort or mergesort.