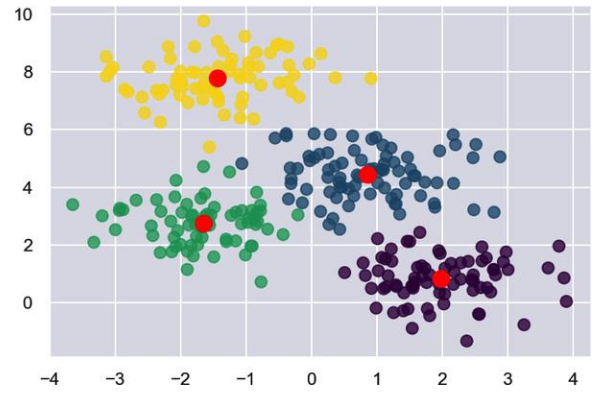
Please share some MCQs for kMeans algo.
Multiple Choice Questions (MCQs) on k-Means Clustering
-
What does k represent in the k-Means clustering algorithm?
a) The number of features in the data
b) The number of data points in the dataset
c) The number of clusters to be formed
d) The distance metric used in the algorithm
-
Which of the following statements is TRUE about the k-Means algorithm?
a) It guarantees finding the optimal cluster centroids in every run.
b) It requires the number of clusters (k) to be specified beforehand.
c) It can handle clusters of arbitrary shapes.
d) It is a supervised learning algorithm that requires labeled data.
-
What is the main objective function minimized during the k-Means clustering algorithm?
a) The accuracy of the model on a validation set
b) The distance between all data points and the nearest cluster centroid.
c) The sum of squared distances between each data point and its assigned cluster centroid.
d) The entropy of the cluster assignments.
-
Which of the following is NOT a common initialization technique for k-Means clustering?
a) Random assignment of data points to clusters.
b) K-means++: A more sophisticated initialization that aims for better spread of initial centroids.
c) Hierarchical clustering followed by splitting the clusters into k groups.
d) Using domain knowledge to pre-define initial centroids.
-
How is the k-Means algorithm sensitive to the choice of the initial cluster centroids?
a) It doesn't affect the final clustering outcome; kMeans always converges to the same clusters.
b) Different initializations can lead to different local minima, potentially impacting the final clusters.
c) It only affects the number of iterations required for the algorithm to converge.
d) Sensitivity to initial centroids is only an issue for high-dimensional data.
-
Which of the following is NOT a suitable evaluation metric for the performance of k-Means clustering?
a) Silhouette score: Measures the average distance between a point and points in its own cluster compared to points in other clusters.
b) Calinski-Harabasz index: Ratio of the between-cluster variance to the within-cluster variance.
c) Accuracy: More appropriate for classification tasks with labeled data.
d) Davies-Bouldin index: Compares the within-cluster scatter to the distance between cluster centers.
Some complex scenario based questions for kMeans.
Complex Scenario-Based Questions for k-Means Clustering
These questions go beyond basic definitions and delve into applying k-Means in challenging situations:
-
Clustering Customer Segmentation: You're tasked with segmenting customers based on their purchase history data (amount spent, frequency, product categories). However, the data contains outliers, representing customers with very high or very low purchase behavior. How would you handle these outliers before applying k-Means clustering for customer segmentation?
-
Clustering Text Documents: You want to cluster a large collection of text documents based on their topics. However, the documents vary greatly in length and vocabulary. How can you pre-process the text data to make it suitable for k-Means clustering of topics?
-
Dynamic k-Means for Streaming Data: Imagine a system that receives real-time sensor data from multiple sources. You want to use k-Means to dynamically cluster the incoming data points to identify emerging patterns. How can you adapt k-Means to handle a continuous stream of data without retraining the entire model every time a new data point arrives?
-
Combining k-Means with Other Algorithms: Suppose you're clustering images based on their visual content using k-Means. You then want to further classify the clusters into specific categories (e.g., landscapes, portraits, objects). How can you combine k-Means with a supervised learning algorithm like a Support Vector Machine (SVM) to achieve this two-stage clustering and classification approach?
-
Choosing the Optimal Number of Clusters (k): k-Means requires specifying the number of clusters (k) beforehand. However, it can be challenging to determine the optimal k value. Discuss different techniques you can use to evaluate and choose the best k for your specific dataset and clustering task.
Solve this:
Clustering Customer Segmentation: You're tasked with segmenting customers based on their purchase history data (amount spent, frequency, product categories). However, the data contains outliers, representing customers with very high or very low purchase behavior. How would you handle these outliers before applying k-Means clustering for customer segmentation?
Discuss the impact of outliers on the cluster formation.
Handling Outliers in Customer Segmentation with k-Means
Outliers in customer purchase history data, representing very high or very low spending behavior, can significantly impact k-Means clustering for customer segmentation. Here's how to handle them:
Impact of Outliers:
- Distort Centroids: Outliers can pull cluster centroids towards them, leading to clusters that don't represent the majority of customers' behavior accurately. This can create skewed segments with unrepresentative characteristics.
- Reduce Cluster Separation: Outliers can make it difficult to distinguish between genuine clusters, especially if they fall between existing clusters. This can lead to poorly defined customer segments.
- Dominate Within-Cluster Variance: Outliers can inflate the within-cluster variance, making it appear like a cluster with high variation even if it contains regular customers with similar behavior.
Strategies for Handling Outliers:
-
Data Cleaning (cautiously):
- Identify outliers statistically (e.g., Interquartile Range (IQR) method) or visually (e.g., boxplots).
- Caution: Removing outliers can discard valuable data points representing genuine, albeit rare, customer behavior. Only remove outliers if you're confident they are errors or irrelevant to your segmentation goals.
-
Capping/Winsorizing:
- Instead of removing outliers, cap their values to a certain threshold within the reasonable range of purchase behavior. Winsorizing replaces extreme values with values at the tails of the distribution (e.g., replacing highest/lowest 5% with the next highest/lowest non-outlier values).
- This approach retains information from outliers while reducing their impact on the clustering process.
-
Standardization/Normalization:
- Standardize (z-score) or normalize (min-max scaling) the purchase amount and frequency features. This reduces the influence of outliers based on the scale of the data, making them less impactful on distance calculations in k-Means.
-
Robust k-Means Variants:
- Explore k-Means variations like k-Medians or Mini-Batch k-Means that are less sensitive to outliers by using median distances or processing data in smaller batches.
Choosing the Right Approach:
The best approach depends on the nature of your data and the number of outliers. Consider:
- The severity of the outliers: Are they extreme outliers or just slightly outside the typical range?
- The volume of outliers: How many outliers are there compared to the total number of customers?
- The potential loss of information: Removing outliers might discard valuable customer segments.
Always evaluate the impact of your chosen approach on the resulting customer segments. Analyze the cluster characteristics to ensure they represent meaningful customer groups.
Can you show some example code to run k-Medians and mini batch k-means?
Running k-Medians and Mini-Batch k-Means with Python
Here's an example using scikit-learn to demonstrate k-Medians and Mini-Batch k-Means for customer segmentation:
1. Sample Data (Replace with your actual purchase data):
Python# Sample customer data (ID, purchase amount, purchase frequency)
customer_data = [
[1, 100, 2],
[2, 500, 1],
[3, 20, 4],
[4, 8000, 1], # Outlier (high spend)
[5, 30, 3],
# ... more customer data
]
# Extract features (amount, frequency)
X = [[row[1], row[2]] for row in customer_data]
2. k-Medians:
Pythonfrom sklearn.cluster import KMedians
# Define the number of clusters (k)
k = 3
# Create and fit the k-Medians model
model = KMedians(n_clusters=k)
model.fit(X)
# Get cluster labels for each customer
cluster_labels = model.labels_
# Assign customers to segments based on cluster labels
segments = {}
for i, label in enumerate(cluster_labels):
if label not in segments:
segments[label] = []
segments[label].append(customer_data[i][0]) # Use customer ID for reference
# Analyze the segments (number of customers, average purchase amount/frequency)
for segment, customer_ids in segments.items():
print(f"Segment {segment+1}: {len(customer_ids)} customers")
# Calculate average purchase amount/frequency here (based on customer data)
3. Mini-Batch k-Means:
Pythonfrom sklearn.cluster import MiniBatchKMeans
# Define the number of clusters (k) and mini-batch size
k = 3
batch_size = 100 # Adjust based on data size and memory constraints
# Create and fit the Mini-Batch k-Means model
model = MiniBatchKMeans(n_clusters=k, batch_size=batch_size)
model.fit(X)
# Get cluster labels (same approach as k-Medians)
cluster_labels = model.labels_
segments = {}
for i, label in enumerate(cluster_labels):
if label not in segments:
segments[label] = []
segments[label].append(customer_data[i][0])
# Analyze the segments (similar to k-Medians)
for segment, customer_ids in segments.items():
print(f"Segment {segment+1}: {len(customer_ids)} customers")
# Calculate average purchase amount/frequency here
Note:
- This is a basic example. Remember to replace the sample data with your actual customer purchase data.
- Explore additional functionalities like outlier handling and evaluation metrics for a more robust customer segmentation process.
Can you explain the working of mini batch kmeans?
Here's an explanation of how Mini-Batch k-Means works:
Standard k-Means Recap:
- Processes the entire dataset in each iteration.
- Calculates the distance between each data point and all cluster centroids.
- Assigns each data point to the closest centroid.
- Updates the cluster centroids based on the assigned data points.
- Repeats these steps until convergence (centroids no longer change significantly).
Limitations of Standard k-Means:
- Can be computationally expensive for large datasets, requiring significant memory to store all data points at once.
- May not be suitable for real-time or streaming data applications.
Mini-Batch k-Means Approach:
-
Sample Mini-Batches: Randomly samples a small subset of data points from the entire dataset (mini-batch). This size is typically much smaller than the whole dataset and can be processed efficiently in memory.
-
Partial Updates: Performs the k-Means steps (distance calculation, assignment, centroid update) on the mini-batch data only. This provides an approximate update for the cluster centroids.
-
Repeat with Different Batches: In each iteration, a new mini-batch is sampled and used to update the centroids. This process continues for a pre-defined number of iterations or until convergence is reached (similar to standard k-Means).
-
Convergence: Mini-Batch k-Means converges to a locally optimal solution, similar to standard k-Means. The quality of the solution depends on the number of iterations, mini-batch size, and the randomness in sampling batches.
Benefits of Mini-Batch k-Means:
- Reduced Memory Consumption: Processes data in smaller chunks, making it suitable for large datasets that might not fit in memory entirely.
- Faster Training: Processing mini-batches can be faster than iterating over the entire dataset, especially for large datasets.
- Potential for Parallelization: Mini-batch updates can be potentially parallelized across multiple cores or machines for even faster processing.
Trade-offs:
- Accuracy: Mini-Batch k-Means might not achieve the same level of accuracy as standard k-Means due to the approximate nature of updates based on mini-batches.
- Choice of Batch Size: A smaller batch size can lead to more noise in the updates and potentially slower convergence. A larger batch size reduces noise but approaches the memory limitations of standard k-Means.
Overall, Mini-Batch k-Means offers a good balance between memory usage, speed, and accuracy for clustering large datasets. It's a popular choice for k-Means applications where processing the entire data at once is impractical.
Solve this:
Clustering Text Documents: You want to cluster a large collection of text documents based on their topics. However, the documents vary greatly in length and vocabulary. How can you pre-process the text data to make it suitable for k-Means clustering of topics?
Here's how you can pre-process text data to make it suitable for k-Means clustering of topics in documents with varying lengths and vocabularies:
1. Text Cleaning:
- Lowercasing: Convert all text to lowercase to avoid case sensitivity.
- Punctuation Removal: Remove punctuation marks that don't contribute to the meaning, like commas, periods, quotation marks, etc.
- Stop Word Removal: Remove common stop words (e.g., "the", "a", "an", "is") that don't hold much topic-specific meaning. Consider domain-specific stop words if applicable (e.g., "research" in academic documents).
2. Text Normalization (Optional):
- Stemming or Lemmatization: Reduce words to their root form (stemming) or base form (lemmatization). This helps group similar words with different prefixes or suffixes (e.g., "running", "runs", "ran" become "run"). Choose stemming for simpler but potentially more aggressive reduction or lemmatization for a more accurate but computationally expensive approach.
3. Feature Extraction:
Instead of using raw word counts, which can be dominated by frequent but not necessarily topic-specific words, consider these techniques:
-
TF-IDF (Term Frequency-Inverse Document Frequency): This assigns weights to words based on their frequency within a document (TF) and their rarity across the entire document collection (IDF). Words that appear frequently in a document but rarely overall get lower weights, reducing the impact of common words and emphasizing words that distinguish topics.
-
Word Embeddings: Techniques like Word2Vec or GloVe learn vector representations of words that capture semantic similarities. Documents can be represented by averaging the word embeddings of their constituent words. This allows k-Means to cluster documents based on semantic relationships between the words they contain, even if the exact words differ.
4. Dimensionality Reduction (Optional):
If the feature vectors from TF-IDF or word embeddings are high-dimensional, consider dimensionality reduction techniques like Principal Component Analysis (PCA) to reduce the number of features while preserving most of the information relevant for topic clustering. This can improve the efficiency and performance of k-Means in high-dimensional spaces.
Choosing the Right Techniques:
The choice of pre-processing steps depends on the characteristics of your text data and the desired level of detail in topic clusters. Here are some general guidelines:
- Start with basic cleaning (lowercasing, punctuation removal) and stop word removal.
- Consider stemming/lemmatization if grammatical variations are important for topic distinction.
- TF-IDF is a common and effective choice for feature extraction.
- Word embeddings can be more powerful but require more training data and computational resources.
- Dimensionality reduction might be helpful with high-dimensional TF-IDF or word embedding vectors, but it can also lead to information loss.
By applying these pre-processing techniques, you can transform your raw text data into a more suitable format for k-Means clustering, allowing it to effectively group documents based on their underlying topics.
Solve this:
Dynamic k-Means for Streaming Data: Imagine a system that receives real-time sensor data from multiple sources. You want to use k-Means to dynamically cluster the incoming data points to identify emerging patterns. How can you adapt k-Means to handle a continuous stream of data without retraining the entire model every time a new data point arrives?
Standard k-Means is not ideal for real-time streaming data due to the need to retrain on the entire dataset for each new data point. Here are some approaches for dynamic k-Means on streaming sensor data:
- Mini-Batch k-Means with Early Stopping:
- Use a mini-batch approach similar to what we discussed earlier. Process data in small chunks and update the centroids based on the mini-batch.
- Implement early stopping to avoid unnecessary iterations within each mini-batch update. This can be achieved by monitoring the change in centroids or the within-cluster variance. If the change falls below a threshold, stop iterating and move to the next mini-batch.
- Incremental k-Means:
- This approach maintains a set of micro-clusters that summarize the data seen so far. These micro-clusters can be represented by centroids and counts/variances.
- When a new data point arrives:
- Assign it to the closest micro-cluster based on distance.
- Update the corresponding micro-cluster's centroid and statistics (count/variance) to incorporate the new data point.
- Periodically (or when a certain number of data points arrive), merge similar micro-clusters based on a distance threshold. This merging helps maintain a manageable number of micro-clusters and prevents them from becoming too granular.
- Optionally, periodically re-initialize a small number of k-Means centroids from the existing micro-clusters to capture large-scale shifts in the data distribution.
- CluStream (Clustering Stream):
- CluStream is a more sophisticated online clustering algorithm that maintains micro-clusters similar to Incremental k-Means, but it also tracks the history of cluster centers.
- This allows it to handle concept drift, where the underlying data distribution changes over time.
- CluStream can forget old data points and adapt to evolving data patterns in the stream.
Choosing the Right Approach:
The choice depends on factors like:
- Data arrival rate: For very high data rates, mini-batch k-Means with early stopping might be efficient.
- Concept drift: If the data distribution changes significantly over time, consider CluStream.
- Computational resources: Incremental k-Means and mini-batch k-Means are generally less resource-intensive than CluStream.
Additional Considerations:
- Outlier Handling: Implement outlier detection and handling techniques to avoid them significantly impacting the cluster updates in the streaming setting.
- Evaluation: Regularly evaluate the quality of the clusters using metrics like silhouette score or Davies-Bouldin index to ensure they capture meaningful patterns in the data stream.
By adapting k-Means with these techniques, you can create a dynamic clustering system that can analyze and react to real-time sensor data streams, helping you identify emerging trends and patterns as they occur.
Can you share code for incremental kmeans?
This is a bit overly complex. Skip it and move on to the next topic if you want...
Here's an example implementation of a basic Incremental k-Means algorithm for streaming data using Python:
Pythonclass IncrementalKMeans:
def __init__(self, n_clusters):
self.n_clusters = n_clusters
self.micro_clusters = [] # List of (centroid, count, variance) tuples
def update(self, data_point):
# Find closest micro-cluster
closest_cluster = min(self.micro_clusters, key=lambda c: distance(data_point, c[0]))
closest_centroid, count, variance = closest_cluster
# Update closest micro-cluster
new_centroid = update_centroid(data_point, closest_centroid, count + 1)
new_variance = update_variance(data_point, closest_centroid, variance, count)
self.micro_clusters.remove(closest_cluster)
self.micro_clusters.append((new_centroid, count + 1, new_variance))
def merge_clusters(self, distance_threshold):
# Merge micro-clusters that are too close
merged = False
for i in range(len(self.micro_clusters) - 1):
for j in range(i + 1, len(self.micro_clusters)):
centroid1, _, _ = self.micro_clusters[i]
centroid2, _, _ = self.micro_clusters[j]
if distance(centroid1, centroid2) <= distance_threshold:
# Merge clusters i and j
merged_centroid, merged_count, merged_variance = merge_micro_clusters(self.micro_clusters[i], self.micro_clusters[j])
self.micro_clusters[i] = (merged_centroid, merged_count, merged_variance)
del self.micro_clusters[j]
merged = True
break
if merged:
self.micro_clusters = self.micro_clusters[:i+1] + self.micro_clusters[i+2:]
def get_cluster_labels(self, data_point):
# Assign data point to closest micro-cluster based on centroid distance
distances = [distance(data_point, c[0]) for c in self.micro_clusters]
return distances.index(min(distances))
# Helper functions for distance calculation, centroid/variance update, and micro-cluster merging (implementation details omitted for brevity)
def distance(p1, p2):
# ... Euclidean distance or other appropriate distance metric
def update_centroid(data_point, centroid, count):
# ... Update centroid based on new data point
def update_variance(data_point, centroid, variance, count):
# ... Update variance based on new data point
def merge_micro_clusters(cluster1, cluster2):
# ... Combine centroids, counts, and variances of two micro-clusters
Explanation:
- This code defines an
IncrementalKMeans class with methods for updating and managing micro-clusters.
- The
update method takes a new data point and assigns it to the closest existing micro-cluster. It then updates the centroid and variance of that micro-cluster to incorporate the new information.
- The
merge_clusters method periodically checks for micro-clusters that are too close (based on a distance threshold) and merges them to maintain a manageable number of clusters.
- The
get_cluster_labels method assigns a new data point to the closest micro-cluster based on centroid distance.
Note:
- This is a simplified example. Real-world implementations might include additional features like outlier handling, forgetting old data points (concept drift), and re-initialization strategies.
- The code snippets for distance calculation, centroid/variance update, and micro-cluster merging are omitted for brevity but can be implemented based on the chosen distance metric and data representation.
By using this approach, you can incrementally update your clustering model as new sensor data arrives in real-time, allowing you to continuously monitor and analyze the evolving patterns in the data stream.
Solve this:
Combining k-Means with Other Algorithms: Suppose you're clustering images based on their visual content using k-Means. You then want to further classify the clusters into specific categories (e.g., landscapes, portraits, objects). How can you combine k-Means with a supervised learning algorithm like a Support Vector Machine (SVM) to achieve this two-stage clustering and classification approach?
Here's how you can combine k-Means with SVM for image classification:
1. Feature Extraction:
- Extract features from your images that represent their visual content. Common features include:
- Color histograms: Capture the distribution of colors in the image.
- SIFT (Scale-Invariant Feature Transform) or SURF (Speeded Up Robust Features): Detect keypoints and their descriptors that are robust to image transformations like scaling and rotation.
- Convolutional Neural Network (CNN) features: If you have a pre-trained CNN model, extract features from intermediate layers that capture high-level visual concepts.
2. k-Means Clustering:
- Apply k-Means clustering to the extracted image features. Choose the number of clusters (k) based on the desired granularity of your initial grouping (e.g., landscapes, portraits, objects might be a good starting point, but k could be higher for finer distinctions).
3. Labeled Data Preparation:
- Prepare a separate dataset of labeled images for each category you want to classify the clusters into (e.g., landscapes, portraits, objects). Ensure these labeled images are representative of the visual characteristics you expect to find in each category.
4. Feature Extraction for Labeled Data:
- Extract the same features (color histograms, SIFT/SURF, or CNN features) from the labeled images.
5. Train an SVM Classifier:
- Train an SVM classifier using the features from the labeled images. Each image belongs to a specific category, providing the labels for supervised learning.
- During training, the SVM learns a decision boundary that separates the features of different categories in the feature space.
6. Classification of k-Means Clusters:
- Take the centroids of each k-Means cluster (which represent the "average" feature vector of the images in that cluster).
- Feed these centroids as input to the trained SVM classifier.
- The SVM will predict the category label (e.g., landscape, portrait, object) for each k-Means cluster based on the features it learned during training.
Benefits:
- Leverages k-Means for Unsupervised Grouping: k-Means helps group images with similar visual content without requiring labeled data initially.
- Improves Classification with SVM: The SVM classifier provides more accurate category labels for the k-Means clusters by leveraging the labeled data.
Considerations:
- Choice of k: The number of k-Means clusters can impact the classification accuracy. Experiment with different k values to find an optimal balance between capturing meaningful groupings and providing enough data for the SVM to learn effectively.
- SVM Hyperparameter Tuning: Tune the hyperparameters of the SVM classifier (e.g., kernel function, regularization) to optimize its performance on the labeled data.
This combination allows you to leverage the unsupervised learning capabilities of k-Means for initial grouping and the supervised learning power of SVM for accurate category classification of the resulting clusters.
Solve this:
Choosing the Optimal Number of Clusters (k): k-Means requires specifying the number of clusters (k) beforehand. However, it can be challenging to determine the optimal k value. Discuss different techniques you can use to evaluate and choose the best k for your specific dataset and clustering task.
Here are some techniques to evaluate and choose the optimal number of clusters (k) for k-Means clustering:
1. Elbow Method:
- This is a visual approach where you run k-Means for a range of k values and plot the Within-Cluster Sum of Squared Errors (WCSS) on the y-axis and the number of clusters (k) on the x-axis.
- WCSS represents the sum of the squared distances between each data point and its assigned cluster centroid. As k increases, WCSS naturally decreases because more clusters are formed, potentially capturing more variations within each cluster.
- The elbow method looks for an "elbow" point in the curve. The ideal k value is often chosen just before this elbow where the rate of decrease in WCSS starts to diminish significantly. This suggests that adding more clusters isn't providing a significant improvement in explaining the data's variance within clusters.
2. Silhouette Score:
- This metric calculates a score for each data point that lies between -1 and 1.
- A score closer to 1 indicates the data point is well-clustered within its assigned cluster, with a large separation from points in other clusters.
- A score near 0 indicates the data point is on the border of clusters and could be assigned to either.
- A negative score suggests the data point might be incorrectly assigned.
- The average silhouette score across all data points is calculated. A higher average score indicates a better clustering solution with well-separated clusters. You can experiment with different k values and choose the one that leads to the highest average silhouette score.
3. Calinski-Harabasz Index:
- This index compares the between-cluster variance to the within-cluster variance. A higher index value indicates a better separation between clusters.
- Similar to the silhouette score, you can calculate this index for different k values and choose the one that maximizes the Calinski-Harabasz index, suggesting well-separated clusters.
4. Gap Statistic:
- This is a more statistically rigorous approach that compares the WCSS of your data with the WCSS of a null distribution generated by randomly shuffling the data labels.
- The gap statistic is calculated for a range of k values. The optimal k is often chosen where the gap statistic reaches a local maximum, suggesting a significant difference between the actual clustering and the random shuffling baseline.
Choosing the Right Technique:
There's no single "best" method for all scenarios. Consider these factors when choosing:
- Dataset Size and Complexity: Elbow method might be suitable for smaller datasets, while silhouette score, Calinski-Harabasz index, or Gap statistic might be more reliable for larger or more complex datasets.
- Interpretability: Elbow method is visual and easy to interpret, while Gap statistic can be computationally expensive and less intuitive.
Additional Tips:
- Often, these techniques provide a range of possible k values. Domain knowledge about the expected number of clusters in your data can help refine the choice.
- You can also run k-Means with different k values and visually inspect the resulting clusters to see if they make sense in the context of your data and problem.
By using a combination of these techniques and considering your specific data and clustering goals, you can make a more informed decision about the optimal number of clusters (k) for your k-Means application.
What is inertia wrt kMeans?
Inertia, in the context of k-Means clustering, refers to the Within-Cluster Sum of Squared Errors (WCSS). It measures the total squared distance between each data point and its assigned cluster centroid within a k-Means clustering solution.
Here's a breakdown of the concept:
- Within-Cluster Variance: This measures how spread out the data points are within a particular cluster. A lower variance indicates the data points are tightly clustered around the centroid.
- Squared Errors: When calculating the distance between a data point and its centroid, we square the distance value. This emphasizes larger distances more than smaller ones.
- Summing Up: WCSS (Inertia) is calculated by summing the squared distances of all data points to their respective cluster centroids in the k-Means solution.
What Inertia Tells Us:
- Lower Inertia: Generally indicates a better clustering solution. It suggests the data points are well-grouped within their assigned clusters, with centroids effectively representing the "center" of each cluster.
- Higher Inertia: Can indicate several possibilities:
- Wrong number of clusters (k): Too few clusters might force data points from naturally distinct groups into the same cluster, leading to higher inertia. Conversely, too many clusters might create small, isolated clusters with high variance within them.
- Outliers: Data points that are significantly different from the majority of the data can pull the centroids towards them, increasing the overall distance between data points and their centroids.
How Inertia is Used:
- Evaluating k-Means Results: Inertia is often used to compare k-Means solutions with different numbers of clusters (k). The k value that results in the lowest inertia is typically considered the "optimal" solution in terms of minimizing the within-cluster variance.
- Monitoring Convergence: During the k-Means algorithm, inertia is calculated in each iteration. As the centroids update and data points are assigned to their closest centers, the inertia typically decreases. This helps monitor the convergence process and determine when the centroids have stabilized.
Note: Inertia is not the only metric for evaluating k-Means clustering. Other techniques like the Elbow Method, Silhouette Score, and Calinski-Harabasz Index are also used to assess the quality and choose the optimal number of clusters.
Ref: Page 26. Chapter 1: Machine Learning. Book by Jeff Prosise: Applied Machine Learning and AI for Engineers (Release 1) - O'Reilly (2022)
