MCQs and Complex Scenario Based Questions on Decision Tree Regressor

Index For Job Interviews Preparation

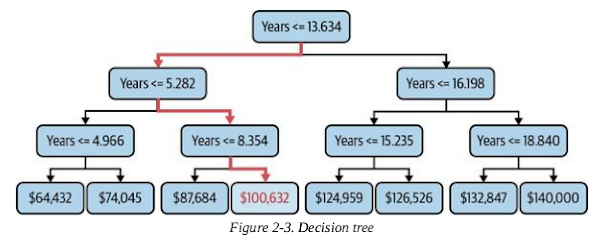
Decision Tree to Model: Years-of-Experience vs. Salary 



The prediction surface from a DecisionTreeRegressor:



Share some MCQs on DecisionTreeRegressor

Multiple Choice Questions on DecisionTreeRegressor
Here are some multiple choice questions (MCQs) to test your understanding of DecisionTreeRegressor in scikit-learn:


Which of the following is NOT a splitting criterion used by DecisionTreeRegressor?
a) Mean squared error (MSE)
b) Information gain
c) Gini impurity
d) Root mean squared error (RMSE)


What parameter in DecisionTreeRegressor controls the maximum depth of the tree?
a) min_samples_split
b) max_depth
c) min_samples_leaf
d) criterion


What is the purpose of the min_samples_split parameter in DecisionTreeRegressor?
a) It determines the minimum number of samples required to split a node.
b) It specifies the minimum number of samples required at a leaf node.
c) It sets the maximum depth of the tree.
d) It defines the splitting criterion used for decision making.


What is the advantage of using DecisionTreeRegressor compared to linear regression models for certain tasks?
a) Decision trees can capture non-linear relationships between features and the target variable.
b) Decision trees are always more accurate than linear regression models.
c) Decision trees require less data to train compared to linear regression models.
d) Decision trees are inherently more interpretable than linear regression models.


What is a potential drawback of decision trees?
a) Decision trees are not suitable for handling categorical features.
b) Decision trees can suffer from overfitting, especially with high-dimensional data.
c) Decision trees are computationally expensive to train compared to linear regression models.
d) Decision trees cannot be used for regression tasks.

Answer Key:

d) Root mean squared error (RMSE) (RMSE is a metric, not a splitting criterion)
b) max_depth
a) It determines the minimum number of samples required to split a node.
a) Decision trees can capture non-linear relationships between features and the target variable.
b) Decision trees can suffer from overfitting, especially with high-dimensional data.


What is the advantage of setting "min_samples_split"?

The main advantage of setting min_samples_split in a DecisionTreeRegressor is to prevent overfitting and improve the model's generalization ability. Here's how it works:

Decision Trees and Overfitting: Decision trees can potentially overfit the training data, especially with high-dimensional datasets. This means the tree becomes too specific to the training data and performs poorly on unseen data.
Role of min_samples_split: This parameter sets a minimum number of samples required to split a node (decision point) in the tree. By requiring a minimum number of samples at each split, you avoid creating overly specific branches based on noise or small fluctuations in the data. This helps to:

Reduce Variance: By ensuring a minimum number of samples at each split, the tree is less likely to make decisions based on random fluctuations in the training data. This leads to a more stable and generalizable model.
Prevent Leaf Nodes with Few Samples: With min_samples_split, you prevent creating leaf nodes (terminal nodes) with very few data points. These leaf nodes might not represent the broader trends in the data and can lead to poor predictions for unseen data.


In essence, setting min_samples_split helps the decision tree focus on learning robust patterns from the data instead of memorizing specific details that might not generalize well to unseen examples.
Here are some additional points to consider:

The optimal value for min_samples_split depends on the size and complexity of your dataset. Experiment with different values and evaluate the model's performance on a held-out test set to find the best setting.
There's a trade-off between preventing overfitting and reducing training efficiency. A very high min_samples_split could lead to underfitting (failing to capture important patterns), while a very low value might not provide enough protection against overfitting.


What other parameters are there for tuning a DecisionTreeRegressor?

DecisionTreeRegressor in scikit-learn offers several parameters for tuning the model's behavior and performance. Here are some key parameters beyond min_samples_split that you can adjust to optimize your decision tree:
Stopping Criteria:

max_depth: This parameter controls the maximum depth of the tree. A deeper tree can capture more complex relationships but is also more prone to overfitting. Experiment with different values to find the sweet spot between complexity and generalization.
min_samples_leaf: This sets the minimum number of samples required at a leaf node. Similar to min_samples_split, it helps prevent overfitting by avoiding overly specific leaf nodes based on few data points.
Splitting Criteria:

criterion: This defines the function used to measure the quality of a split at each node. Common options include "gini" (Gini impurity) for classification and "mse" (mean squared error) for regression tasks. You can experiment with different criteria to see which one improves performance for your specific problem.
Regularization:

max_features: This parameter controls the number of features considered at each split. A lower value can help reduce overfitting by preventing the tree from focusing on irrelevant features. However, setting it too low might prevent the tree from capturing important relationships.
Other Parameters:

random_state: Setting a random seed for random_state ensures reproducibility when training the decision tree multiple times with different hyperparameter configurations.
Tuning Techniques:
Once you've identified relevant parameters, consider techniques like grid search or randomized search to efficiently explore different parameter combinations and find the optimal configuration for your dataset.
By understanding and adjusting these parameters, you can effectively tune your DecisionTreeRegressor to achieve better performance and prevent overfitting. Remember to evaluate the model's performance on a held-out test set to avoid overfitting to the training data.

Share some scenario based questions for DecisionTreeRegressor.

Scenario-Based Questions for DecisionTreeRegressor:
Here are some questions that explore using DecisionTreeRegressor in various scenarios:


Customer Churn Prediction: You're building a model to predict customer churn for a telecommunications company. The features include tenure with the company, monthly call volume, service plan type, and customer satisfaction score. How can you use DecisionTreeRegressor to identify the key factors influencing customer churn?

Solution:

Train a DecisionTreeRegressor with the target variable being a binary indicator of churn (0 for not churned, 1 for churned).
Analyze the feature importance scores provided by the model to understand which features (tenure, call volume, etc.) have the most significant influence on churn predictions.
Visualize the decision tree to gain insights into the decision-making process for churn prediction.





Housing Price Estimation: You're developing a model to estimate housing prices based on features like square footage, number of bedrooms, location, and year built. How can you handle potential non-linear relationships between features and price using DecisionTreeRegressor?

Solution:

Decision trees can inherently capture non-linear relationships by splitting the data based on feature values. Train the DecisionTreeRegressor to predict the continuous target variable (housing price).
Evaluate the model's performance on a held-out test set using metrics like mean squared error or R-squared.
Consider comparing the performance of DecisionTreeRegressor with other models like Random Forest or Support Vector Machines with suitable kernels, which might be better suited for non-linear problems with larger datasets.
 
 
 




Anomaly Detection in Sensor Data: You're analyzing sensor data from a factory to detect anomalous readings that might indicate equipment malfunctions. The sensor readings are continuous numerical values. How can you use DecisionTreeRegressor for anomaly detection?

Solution:

Train a DecisionTreeRegressor to predict the typical sensor readings based on historical data.
Identify data points that fall outside the decision tree's predictions (deviations from the learned patterns) as potential anomalies.
Fine-tune the model parameters (min_samples_split, max_depth) to balance capturing normal variations and identifying true anomalies.




Remember, these are just a few examples. DecisionTreeRegressor can be applied to various scenarios where understanding the decision-making process and capturing non-linear relationships add value to the modeling task.

Can you show it through code the use case of Anamoly Detection in Sensor Data using DecisionTreeRegressor?

Certainly, here's Python code demonstrating anomaly detection in sensor data using DecisionTreeRegressor:
Python
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor

# Load sensor data (replace with your actual data)
data = pd.read_csv("sensor_data.csv")
sensor_readings = data["sensor_reading"]  # Feature (sensor readings)

# Split data into training and testing sets
X_train, X_test, _, _ = train_test_split(sensor_readings, sensor_readings, test_size=0.2, random_state=42)

# Train DecisionTreeRegressor to predict typical sensor readings
model = DecisionTreeRegressor()
model.fit(X_train.values.reshape(-1, 1), X_train)  # Reshape for single feature

# Predict sensor readings on the test set
predicted_readings = model.predict(X_test.values.reshape(-1, 1))

# Define threshold for anomaly detection (adjust based on data)
threshold = 0.1  # Example threshold, can be standard deviation or a percentile

# Detect anomalies based on prediction errors
anomalies = []
for i, (reading, prediction) in enumerate(zip(X_test, predicted_readings)):
  error = abs(reading - prediction)
  if error > threshold:
    anomalies.append(i)

# Print or process anomaly indices
print(f"Anomaly indices in test set: {anomalies}")

# You can further analyze the sensor data points at these anomaly indices
 Use code with caution.
Explanation:

Import Libraries: We import pandas for data manipulation, train_test_split from sklearn.model_selection to split the data, and DecisionTreeRegressor from sklearn.tree.
Load Data: Replace "sensor_data.csv" with your actual CSV containing a column named "sensor_reading".
Split Data: Split the data into training and testing sets using train_test_split. The test set will be used for anomaly detection.
Train Model: Train the DecisionTreeRegressor model using model.fit(). Reshape the training data (X_train) to a 2D array for compatibility with the model (even though it's a single feature).
Predict Sensor Readings: Predict sensor readings on the test set using model.predict().
Define Anomaly Threshold: Set a threshold for anomaly detection. This could be a fixed value (like 0.1 here), a standard deviation from the predicted value, or a specific percentile.
Detect Anomalies: Iterate through the test set and predicted readings. Calculate the absolute error (difference) between the actual and predicted values. If the error exceeds the threshold, consider the data point an anomaly and append its index to the anomalies list.
Process Anomalies: The code prints the anomaly indices in the test set. You can use these indices to further analyze the corresponding sensor data points to investigate potential equipment malfunctions or unusual readings.
Note:

Adjust the anomaly threshold based on the characteristics of your sensor data and the desired sensitivity for anomaly detection.
This is a basic example. Consider techniques like cross-validation or hyperparameter tuning for a more robust model. You might also explore other anomaly detection algorithms depending on your specific needs.

Tags: Technology,Machine Learning,Regression,Interview Preparation,