2-D Matrix in Python

Indices in a 1D List

1-D List

What is a 2D Matrix?

This 2D matrix has got 3 rows and 3 columns.

Contents of Row 0: A B C

Contents of Row 1: D E F

Contents of Row 2: G H I

Contents of Col 0: A D G

Contents of Col 1: B E H

Contents of Col 2: C F I

Indices in a 2D Matrix of Shape 2 X 2

Indices in a 2D Matrix of Shape 3 X 3

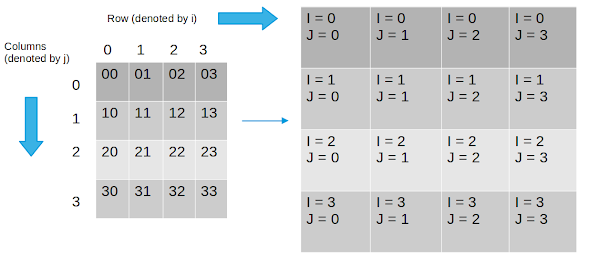
Indices in a 2D Matrix of Shape 4 X 4

Square Matrices And Rectangular Matrices (Part 1)

Matrices of shape: 2X2, 3X3 and 4X4 were square matrices.

Square matrix has same number of rows and columns.

Rectangular matrix has number of rows different from number of columns.

Two columns

Three rows

Shape of a matrix is given by:

Number of rows X Number of cols

Shape of this matrix is: 3X2

Problem on Square Matrices And Rectangular Matrices

Q1: How many rows does it have?

Q2: How many columns does it have?

Q3: What is its shape?

Answers:

1) 3

2) 5

3) Rectangle of shape 3X5

Problem 1

• Ques: Create a 2D matrix programmatically using for loop with following contents:
• [ [1, 2, 3],
• [4, 5, 6],
• [7, 8, 9] ]
• The matrix should not hardcoded but created using for loop.

Solution 1

• [
• [1, 2, 3], # This is your first row
• [4, 5, 6], # This is your second row
• [7, 8, 9] # This is your third row
• ]

r = 3 # Number of rows
c = 3 # Number of columns

mylist = []

cntr = 1

for i in range(r):
# This means loop will run r times.

    temp = []
    for j in range(c):
        temp.append(cntr)
        cntr += 1
    mylist.append(temp)

print(mylist)
    

A 2D matrix is essentially a list of lists.

First, (i) will be 0. (j) will go from 0, 1, 2.

Then, (i) will be 1. (j) will go from 0, 1, 2.

Lastly, (i) will be 2. (j) will go from 0, 1, 2.

import numpy as np

n = np.array(range(1, 10))

n.reshape(3, 3)

Problem 2

• Ques: This matrix is given to you:
• [ [1, 2, 3],
• [4, 5, 6],
• [7, 8, 9] ]
• You have to add 5 to each number in this matrix.
• Addition of 5 to each element in the matrix.

Solution 2

Way 1:

arr = [ [1, 2, 3],
[4, 5, 6],
[7, 8, 9] ]

for i in arr:
    for j in i:
        print(j + 5)

print("Further if we want to create a new array")

mod_arr = []
for i in arr:
    templist = []
    for j in i:
        templist.append(j+5)
    mod_arr.append(templist)

print(mod_arr)

Way 2: Using numpy

import numpy as np
arr = np.array(arr)
arr += 5
print(arr)

[[ 6  7  8]
 [ 9 10 11]
 [12 13 14]]

Problem 3

m = [

[0, 1, 2, 3],

[4, 5, 6, 7],

[8, 9, 10, 11],

[12, 13, 14, 15]

]

""" What is the position of 6?

What is the position of 8?

What is the position of 10?

What is the position of 12?

"""

Solution 3

m = [ [0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11], [12, 13, 14, 15]]

""" What is the position of 6?

Ans: [1][2]

What is the position of 10?

Ans: [2][2]

What is the position of 12?

Ans: [3][0]

"""

Diagonal of a Square Matrix (Top Left to Bottom Right)

Problem: Printing the two diagonals

Print the diagonals:

m = [['A', 'B', 'C', 'D'], ['E', 'F', 'G', 'H'],

['I', 'J', 'K', 'L'], ['M', 'N', 'O', 'P']]

Solution

matrix = [['A', 'B', 'C', 'D'], ['E', 'F', 'G', 'H'], ['I', 'J', 'K', 'L'], ['M', 'N', 'O', 'P']]

# Given a two dim. matrix
rows = cols = len(matrix)

print("Diagonal top-left to bottom-right")
for i in range(rows):
    for j in range(cols):
        if(i == j):
            print(matrix[i][j])

print("Diagonal top-right to bottom-left")
for i in range(rows):
    for j in range(cols):
        if(i + j == rows - 1):
            print(matrix[i][j])    

Printing diagonals using numpy

matrix = [['A', 'B', 'C', 'D'], ['E', 'F', 'G', 'H'], ['I', 'J', 'K', 'L'], ['M', 'N', 'O', 'P']]

matrix = np.array(matrix)

print(matrix)

[['A' 'B' 'C' 'D']

['E' 'F' 'G' 'H']

['I' 'J' 'K' 'L']

['M' 'N' 'O' 'P']]

matrix.diagonal()

array(['A', 'F', 'K', 'P'], dtype='<U1')

# fliplr() : flip left to right

print(np.fliplr(matrix))

print(np.fliplr(matrix).diagonal())

[['D' 'C' 'B' 'A']

['H' 'G' 'F' 'E']

['L' 'K' 'J' 'I']

['P' 'O' 'N' 'M']]

['D' 'G' 'J' 'M']

​

Printing upper triangle and lower triangle

m = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
np.triu(m)

array([[1, 2, 3],
        [0, 5, 6],
        [0, 0, 9]])

np.tril(m)

array([[1, 0, 0],
        [4, 5, 0],
        [7, 8, 9]])

Credits
Aman Kumar
LinkedIn