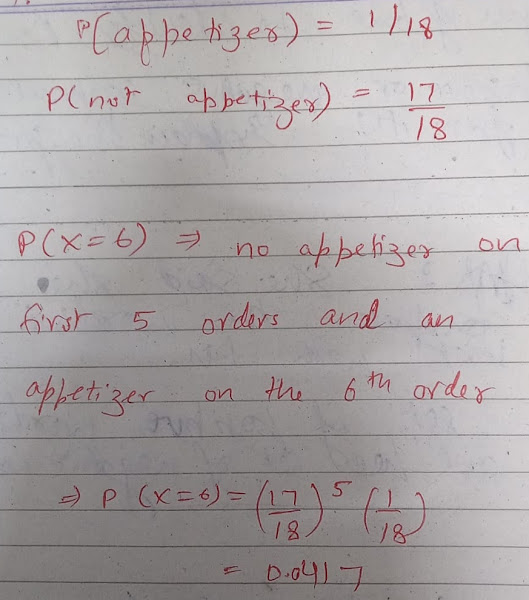Questions on The Concept of Random Variables From Statistics and Probability (From Khan Academy)

1: Random variables

1.1: Constructing probability distributions

Question 1:







Question 2:







1.2: Probability models

Question 3:






2: Probability with discrete random variables

Question 4:






3: Combining random variables

Question 5:







Question 6:







4: Identifying binomial variables

Four Conditions of Binomial Variable

1. There are fixed number of trials.

2. Each trial results in a success of failure.

3. A trial is independent of other trials.

4. Probability of success remains constant over time.

Question 7:







Question 8:







Question 9:







5: Binomial probability formula

Question 10:







Question 11:










Question 12:










6: Calculating binomial probability

Question 13:







Question 14:







7: Binomial vs. geometric random variables

Question 15:




Question 16:




Question 17:




Question 18:




8: Geometric probability

Question 19:







9: Cumulative geometric probability

Question 20:






Question 21:






Question 22:






Question 23:

Tags: Technology,Mathematical Foundations for Data Science,

Data Structures, Algorithms and Coding Round For Data Scientist at Agoda (26 Sep 2023)

Note: problems are ordered in increasing order of complexity.

Problem 1
Problem Description:

You are standing on a unique diamond-shaped platform composed of 5 tiles. These tiles are positioned at coordinates: (-1,0), (0,-1), (0,0), (0,1), and (1,0).

From a starting position (xs,ys), you make random moves in one of four directions: left (decrease x by 1), right (increase x by 1), up (increase y by 1), or down (decrease y by 1). Each direction has the same probability and the direction of each move is entirely independent of previous moves.

Determine the probability that you can reach a given destination (xe,ye) without stepping off the diamond platform.

Constraints:

(xs, ys) must be one of: (-1,0), (0,-1), (0,0), (0,1), (1,0)
(xe, ye) must also be one of the above coordinates.
Starting and ending coordinates are distinct: xs != xe or ys != ye

Input:

A single line containing four integers, denoting xs, ys, xe, ye respectively.

Output:

A single line showing the probability that you'll reach the destination before stepping off the platform.

Sample input:

-1 0 0 0

Sample Output:

0.25

Explanation:

From the starting position, you have a 25% chance of moving right (and thus reaching the destination). Any other move would result in falling off the platform.

    [execution time limit] 4 seconds (py3)

    [memory limit] 1 GB

    [input] integer xs

    The x-coordinate of the starting position.

    [input] integer ys

    The y-coordinate of the starting position.

    [input] integer xe

    The x-coordinate of the end position.

    [input] integer ye

    The y-coordinate of the end position.

    [output] float

    Probability to reach end position before falling of platform.


Problem 2

There are two operators:

    operator1: adds x to current number
    operator2: multiplies current number by y

where the values of x an y are given and fixed. The starting number is 1 and the goal is to get to number t by sequentially applying operator1 and operator2. You have to maximize the number of times you use operator2. For maximum usage of operator 2, you have to minimize the number of times you use operator 1.

Constraints:
2 <= x <= 1000
2 <= y <= 1000
1 <= t <= 10^20

Input: t, x, y

Output in case there is a solution:
List of strings where:

    Element 1: "operator_add" or "operator_multiply" followed by how many times you want to apply it.
    Element 2: "operator_add" or "operator_multiply" followed by how many times you want to apply it to result of previous line.
    ...

The solution should be returned in a compact format in the sense that if element i corresponds to operator_add, then element i+1 corresponds to operator_multiply and vice versa.

Output in case there is no solution:
List with one element: "no_solution".

Sample input:
t = 54
x = 1
y = 3

Sample output:
["operator_add 1", "operator_multiply 3"]

Explanation: ((1 + 1) times 3^3) = 54
Operator2 can be used maximally 3 times because 3^4 > 54. For operator2 being used three times, operator1 needs to be used at least once because 3^3 is not equal to 54.

Sample input:
t = 3
x = 4
y = 4

Sample output:
["no_solution"]

Explanation: every operator increase the number and applying any operator once already results in a number that is too big.

    [execution time limit] 4 seconds (py3)

    [memory limit] 1 GB

    [input] integer64 t

    Target number: the number you want to reach by sequentially applying the operators.

    [input] integer64 x

    By how much you increase the current result if you apply operator1.

    [input] integer64 y

    By how much you multiply the current result if you apply operator2.

    [output] array.string

    List of strings where element i equals "operator_add" or "operator_multiply" followed by how many times you want to apply it. In case there is no solution, output is ["no_solution"].


Problem 3

You want to buy a billboard featuring the name of your company. The price of the billboard is the sum of the price of the letters in your company name. For example, the price of company name "aga" is two times the price of letter "a" plus the price of letter "g". You don't know the price per letter, but you do know the prices of other company names. Can you derive the price of your company name? A company name only contains letters from the alphabet. There are 26 different letters and they are all lower case.

You are given:

    your_company_name: a string representing the name of your company
    other_company_names: a list of strings where each element is the name of another company
    other_company_prices: a list of real numbers where other_company_prices[i] is the price of other_company_names[i]

Return the price of your company name if it can be derived, otherwise return -1

Constraints:
The length of a company name is maximally 100
len(other_company_names) = len(other_company_prices) <= 100
For each price in other_company_prices: -10^6 <= price <= 10^6

Sample Input:
your_company_name = "aabc"
other_company_names = ["ab", "ac", "bd"]
other_company_prices = [99.5, 1000.2, 2000.8]

Sample Output:
1099.7

Explanation: The letters in "aabc" is the union of the letters in "ab" and "ac", hence the price is the sum.

Sample Input:
your_company_name = "d"
other_company_names = ["aab", "acc"]
other_company_prices = [500, 6000]

Sample Output:
-1

Explanation: The letter d doesn't appear in any other company name and therefore we cannot derive its price.

    [execution time limit] 4 seconds (py3)

    [memory limit] 1 GB

    [input] string your_company_name

    String representing the name of your company

    [input] array.string other_company_names

    List containing the names of other companies.

    [input] array.float other_company_prices

    List where element i contains the prices of other_company_names[i]

    [output] float

    Price of your company

Tags: Technology,Algorithms,Interview Preparation,

Similarity, dissimilarity and distance (Part of Data Analytics Course)

Measuring Similarity/Dissimilarity

Briefly outline how to compute the dissimilarity between objects described by the following types of variables:

Numerical (interval-scaled) variables

A = (2, 4)

B = (1, 3)

Euclidean distance = math.sqrt(pow(2-1, 2) + pow(4-3, 2))

A = (2, 7, 5)

B = (4, 8, 9)

ed = math.sqrt(pow(2-4, 2) + pow(7-8, 2) + pow(5-9, 2))

Euclidean distance is the direct and straight line distance.

Whereas:

Manhattan distance is indirect and calculated along x and y axis.

Euclidean Distance

Manhattan Distance

Manhattan Distance

Manhattan Distance is inspired from a traveler going from one point to another in the city of Manhattan.

Euclidean distance: Straight line distance between two points.

Manhattan distance: is cityblock distance that is you would go from place to place in car.

Minkowski Distance

Given two objects represented by the tuples (22, 1, 42, 10) and (20, 0, 36, 8):

Compute the Minkowski distance between the two objects, using p = 3.

In plain English: kth root of sum of kth powers of absolute value of differences.

For manhattan distance, p = 1 in Minkowski dist.

For euclidean distance, p = 2 in Minkowski dist.

Manhattan and Euclidean distances are special cases of Minkowski.

Similarity/Dissimilarity

Briefly outline how to compute the dissimilarity between objects described by:

• Asymmetric binary variables

If all binary attributes have the same weight then they are symmetric. Let’s say we have the contingency table:

If the binary attributes are asymmetric, Jaccard coefficient is often used:

For cell (i=1, j=1) representing #(object I = 1 and object J = 1):

J = q / (q + r + s)

J = # elements in intersection / # elements in the union

Jaccard similarity (aka coefficient or score) ranges from 0 to 1.

Jaccard dissimilarity (aka distance) = 1 – Jaccard Similarity

The reason why ‘t’ is not considered in Jaccard coeff. Is because, while taking an example of shopping cart, it would not make same sense to count the number of times that were missing from both the cart I and J. If we count the number of items that were missing in both carts, it would increase the similarity.

If it is given the attributes are binary and assymmetric, t is not counted. If it is symmetric, then formula for J may include ‘t’ in the numerator and denominator:

J = (q + t) / (q + r + s + t)

Similarity/Dissimilarity

Briefly outline how to compute the dissimilarity between objects described by the following types of variables:

• Categorical variables

A categorical variable is a generalization of the binary variable in that it can take on more than two states.

The dissimilarity between two objects i and j can be computed as:

where m is the number of matches (i.e., the number of variables for which i and j are in the same state), and p is the total number of variables.

Similarity/Dissimilarity

Between text type of data:

This is equal to dot-product of the corresponding features divided by the magnitude. Geometrically, it is equal to the cosine of angle between two lines.

V	D1	D2	D3	D4	D5	D6	D7	D8	D9	D10
A	1	1	0	1	1	0	0	1	1	0
B	1	0	1	0	1	1	1	0	0	0
C	0	1	0	0	1	1	0	1	0	1
D	1	0	0	0	0	1	0	1	0	0
E	1	0	1	0	1	1	0	0	0	0

Cosine similarity is commonly seen in text data.

Which two out of these vectors are closest?

And, which two out of these vectors are farthest?

A	1	1	0	1	1	0	0	1	1	0
B	1	0	1	0	1	1	1	0	0	0
A.B	1	0	0	0	1	0	0	0	0	0

There are two ones so sum()

= 1 + 0 + 0 + 0 + 1 + 0 + 0 + 0 + 0 + 0

= 2

A	1	1	0	1	1	0	0	1	1	0
B	1	0	1	0	1	1	1	0	0	0

|A| = math.sqrt(1**2 + 1**2 + 0 + 1**2 + 1**2 + 0 + 0 + 1**2 + 1**2 + 0)

= 2.449489742783178

|B| = math.sqrt(1**2 + 0 + 1 + 0 + 1 + 1 + 1 + 0 + 0 + 0)

= 2.23606797749979

Cos similarity (A, B) --> cos(theta) = A.B / |A|.|B|

Cosine similarity = 2 / ( 2.449 * 2.236 )

= 0.3652324960500105

A	1	1	0	1	1	0	0	1	1	0
B	1	0	1	0	1	1	1	0	0	0
A.B	1	0	0	0	1	0	0	0	0	0

Cosine Similarity

A = (4, 4)

B = (4, 0)

Cosine similarity between A and B is: cos(theta)

Note: It is very easy to visualize it in 2D.

Formula wise: Cosine similarity = A.B / |A| * |B|

This formula has come after rearranging the dot product formula:

A.B = |A| * |B| * cos(theta)

(0,0)

Cosine Similarity

Find cosine similarity between the following two sentences:

IIT Delhi course on data analytics IIT

IIT Delhi course on data analytics

Term: tf for d1, tf for d2

d1.d2 = 2.1 + 1.1 + 1.1 + 1.1 + 1.1 + 1.1 = 7

|d1| = sqrt(2^2 + 1^2 + 1^2 + 1^2 + 1^2 + 1^2) = sqrt(9)

|d2| = sqrt(1^2 + 1^2 + 1^2 + 1^2 + 1^2 + 1^2) = sqrt(6)

Cosine similarity = d1.d2 / |d1| * |d2| = 7 / sqrt(9*6) = 0.93

IIT	2	1
Delhi	1	1
Course	1	1
On	1	1
Data	1	1
Analytics	1	1

Cosine Similarity

Sent 1: I bought a new car today.

Sent 2: I already have a new car.

Step 1: Create vectors.

	Vector 1	Vector 2	Product of components
I	1	1	1
bought	1	0	0
a	1	1	1
new	1	1	1
car	1	1	1
today	1	0	0
already	0	1	0
have	0	1	0

Cosine Similarity

V1 = 1,1,1,1,1,1,0,0

V2 = 1,0,1,1,1,0,1,1

v1.v2 = 1 + 0 + 1 + 1 + 1 + 0 + 0 + 0 = 4

|v1| = math.sqrt(1**2 + 1**2 + 1**2 + 1**2 + 1**2 + 1**2 + 0 + 0) = 2.45

|v2| = math.sqrt(1**2 + 0 + 1**2 + 1**2 + 1**2 + 0 + 1**2 + 1**2) = 2.45

Cosine sim = 4 / (2.45 * 2.45)

= 0.66

Cosine Similarity

Cosine Similarity: It is a bag-of-words based model i.e., order of words does not matter.

Sent1: I bought a new car today.

Sent2: I haven’t bought a new car today.

Step 1: Creating vectors

Cosine similarity is based on whether same words have been used in two sentences.

“How similar are two sentences in terms of the words (irrespective of their meaning) used in them?”

Cosine Similarity

Find cosine similarity between the following two sentences:

Brand new course on data analytics

Test-1 is scheduled later this month

Cosine similarity = 0.0

In Code Following Steps Would Be Followed To Find The Cosine Similarity Between Two Sentences

1. Load the libraries like Scikit Learn.

Projects might include other libraries like Pandas, NumPy, NLTK (Natural Language Toolkit).

2. Load the data (i.e. your two sentences)

3. Convert them into vector form using CountVectorizer.

Note: there are some other ways also to convert a sentence into vector, but we want to keep it simple for first class.

4. Next, you can use this method: sklearn.metrics.pairwise.cosine_similarity() to find the cosine similarity.

Note: These are high level steps. You can find a lot of similarity/dissimilarity measures following these steps after some minor modifications like changing Scikit Learn with SciPy, etc.

Thank You!

Tags: Technology,Data Analytics,

Python Math Module

# It contains a set of built-in functions and a math module

# Used to perform various mathematical tasks on numbers

# For Ex – Finding minimum and maximum value among multiple numbers

x = min(5, 10, 25)  # Use of built in math 
y = max(5, 10, 25)  # functions

print(x)
print(y) 

Output will be :

5

25

# For Ex – Getting Absolute ( Positive) and Power Values

x = abs(-7.25)
print(x) 

Output will be : 7.25

x = pow(4, 3)
print(x) 

Output will be : 64

# Use of math module functions

# For Ex - Calculating square root value of a number

import math

x = math.sqrt(64)

print(x)

Output will be : 8

# For Ex – Getting the upward and downward nearest integer value of a real number

import math

x = math.ceil(1.4)   # Will return upward nearest number
y = math.floor(1.4)  # Will return downward nearest number

print(x) 
print(y)

Output will be: 
		2
		1

# For Ex – Getting the value of PI Constant

import math

x = math.pi

print(x) 

Output will be: 3.141592653589793

Note * : There are many more functions and constants available to use in math module

Tags: Technology,Python

Python’s Built-in Modules

Python’s Standard Library

It is there so that developers can focus on the task in hand and not sit to re-invent the wheel for common task.

Core Ideas:

- Reusability

- Standardization of code

Some commonly used modules are as given below:

# There is one for Math – as in 'math' used for constants like math.pi

# There is one for Statistics – as in statistics.mean()

# random

# “string” – for string templates like ascii_lower

# collections

# Itertools

# “dateutil” - as in dateutil.parser.parse()

---

import string
string.ascii_lowercase
'abcdefghijklmnopqrstuvwxyz'
l = [chr(i) for i in range(ord('a'), ord('z') + 1)]
print(l)

['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']

s = ""
for i in range(ord('a'), ord('z') + 1): s += chr(i)
print(s)
abcdefghijklmnopqrstuvwxyz    

---

String Classes Available in The Form of String Templates

print(string.digits)

0123456789

#

print(string.ascii_lowercase)

abcdefghijklmnopqrstuvwxyz

#

print(string.ascii_uppercase)

ABCDEFGHIJKLMNOPQRSTUVWXYZ

#

print(string.ascii_letters)

abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ

#

print(string.printable)

0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!"#$%&'()*+,-./:;<=>?@[\]^_`{|}~

#

print(string.hexdigits)

0123456789abcdefABCDEF

#

print(string.octdigits)

01234567

Iterators in Python (Theory)

• An iterator object is used to iterate through all items/values of a Iterable Object
• To iterate we need to get Iterator object from Iterable Object
• iter() and next() method are associated with Iterator object
• String, Tuple, List, Set and Dictionaries all are iterable objects
• There is built in iter() method, that is used to get Iterator object from an iterable object
• We can iterate all items of an iterable object using for loop as well
• For loop automatically create an Iterator object for an iterable object and call next() method for iterating through all items
• To create an object/class as an iterator you have to implement the methods __iter__() and __next__() to your object

Traffic Prediction on my Blog (Oct 2023)

Poisson Distribution for Traffic Prediction in Layman Terms

Imagine you're trying to predict how many cars will pass through a specific point on a road during a certain period, like an hour. The Poisson distribution can help you make this prediction.

Here's how it works in simple terms:

Events Occurring Over Time

The Poisson distribution is used when you're dealing with events that happen randomly over a fixed period of time. In our example, these events are cars passing by.

Average Rate

You start by knowing the average rate at which these events occur. For instance, on average, 30 cars pass by in an hour.

Independence

You assume that the arrival of each car is independent of the others. In other words, one car passing by doesn't affect the likelihood of another car passing by.

Probability of a Specific Number
    
With the Poisson distribution, you can calculate the probability of a specific number of events happening in that fixed time period. So, you can calculate the chance of exactly 25 cars passing by in an hour or any other number.

Shape of Distribution
    
The Poisson distribution has a particular shape that's skewed to the right. It's more likely to have fewer events than the average rate, and less likely to have more events, but it allows for some variability.

On a side note: 
Right skewed: The mean is greater than the median. The mean overestimates the most common values in a positively skewed distribution. Left skewed: The mean is less than the median.

Use in Traffic Prediction

To predict traffic, you can use the Poisson distribution to estimate the likelihood of different traffic volumes. If the average rate is 30 cars per hour, you can calculate the probabilities of having 20 cars, 40 cars, or any other number during that hour. This information can be useful for traffic planning and management.

In summary, the Poisson distribution helps you make educated guesses about the number of random events (like cars passing by) happening in a fixed time period, assuming they occur independently and at a known average rate. It's a valuable tool for predicting and managing things like traffic flow.

Here is how I used it to predict the traffic on my blog

1: Glimpse of the data



2: Tail of the data



3: Frequency plot for views in thousands



4: Number of views in thousands and probability of seeing that many views



5: Poisson distribution for views in thousands



6: Conclusion

# There is ~1.5% chance that there will be 9 thousand views.

# There is ~10% chance that there will be 16 thousand views.

# There is ~7.8% chance that there will be 19 thousand views.
 
Download Code and Data

In the next post, we will see why our analysis could be wrong.

When not to use Poisson Distribution for prediction?

Tags: Technology,Machine Learning,Data Analytics,Python